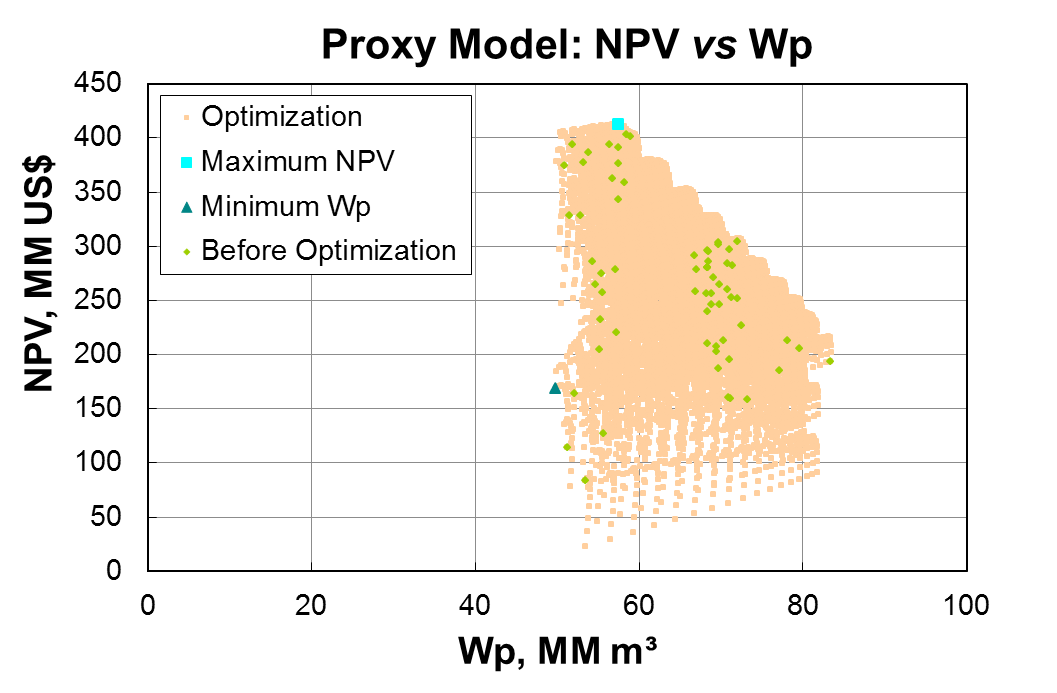
Proxy Models
The steps of petroleum field management require a high effort and computational time, especially for complex models with high heterogeneity, and for probabilistic problems. Sometimes, process of scaling, uncertainty quantification, risk analysis, history matching, optimization and production forecast and decision making require many runs of simulation to search quantified and matched models based on available data in order to provide a reliable production forecast of a petroleum field.
Another important point to note is that the production forecast from adjusted numerical reservoir models are almost invariably "wrong", in which these predictions, in most of the time, do not match the observed production for a relatively short period of time. It is not clear is how wrong they might be in any given scenario, and this fact has led to increased research on quantification of uncertainty in oil reservoirs using mathematical and statistical approaches. In addition, understanding that this uncertainty is crucial for decision-making process at all levels of management of an oil field.
Over the recent years, studies of fast models, proxy models, which are considered low-fidelity ones to "emulate" the numerical reservoir simulator have been developed to speed up a stage of the reservoir management process and consequently reduce the time decision-making. In contrast to techniques based on representative solutions, proxy models, built from mathematical and statistical approaches can, in theory, produce fast and consistent models that can substitute the simulator, high-fidelity model, in the steps of a petroleum reservoir studies. Another important point to highlight is that the quality of proxy model generated will strongly depend on used mathematical approach (algorithm) and the observed data (history) used to build it.
The most used proxy models in the oil industry are: multivariate kriging model (KG); artificial neural network (ANN); polynomial regression models (PRM); response surface methodology (RSM) and emulators (EM).
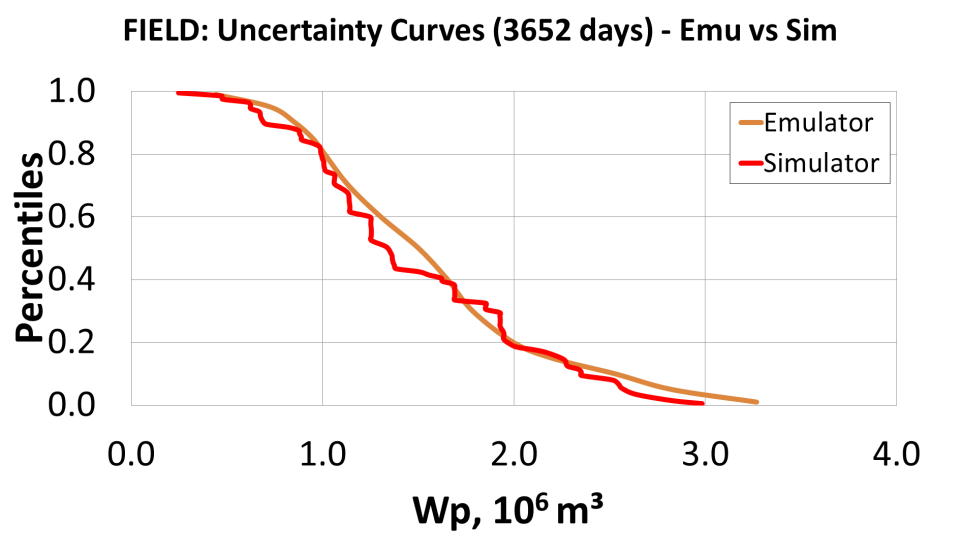
Emulator
Despite the advancement of generation techniques of proxy models over the past decade, there are still many barriers to effective implementation in stages of oil reservoir management. These include the high cost in computational time to quantify probabilistic problems; effective ways to parameterize a geological model to be realistic and easily matching models with the historical data; effective methods to calibrate numerical models from the available field data; analysis of measurement errors of various types of data which the model will be calibrated; and effective techniques for forecasting and decision making. In this context, the emulation technique arises.
This technique builds a statistical model for the errors occurring during the simulation of numerical models of the reservoir, and predicts both a mean error and variance that are used to amend the misfit (or match quality) expression. By including these corrections in the misfit term, the responses estimated by the emulator will tend to stay close to those that would be obtained using a reservoir numerical simulator. In addition to using the emulator to a past period, that is, history data, one can also measure around the forecast production using the emulation technique.
The main challenge of this research is on the speed and effectiveness in which the models will be calibrated by combining Bayes linear emulation approach, developed by Durham University, Department of Mathematical Sciences, Statistics and Probability group of Professor Michael Goldstein, Dr. Ian Vernon at Durham and Dr. Camila Caiado, and statistically accurate stochastic sampling algorithms. The key concept is to make every high computational cost simulation, highlighting learning about the response to the linear method of Bayes. Thus, the key concept here is to make every expensive simulation count, so as we learn about the response surface with the Bayes Linear methodology, we can target our expensive function evaluations in regions where the probability of finding a good fitting model is high. Once there are a number of matched models from the emulation technique, production forecasts will be generated using a valid statistical methodology, with there is another object of study along this line of research.






